Algoritma Floyd Warshall adalah salah satu varian dari pemrograman dinamis, metode untuk memecahkan masalah pencarian rute terpendek (sama seperti Algoritma Dijkstra). Metode ini melakukan pemecahan masalah dengan memandang solusi yang akan diperoleh sebagai suatu keputusan yang saling terkait. Maksudnya, solusi-solusi dibentuk dari solusi yang berasal dari tahap sebelumnya dan ada kemungkinan solusi lebih dari satu. Algoritma ini juga bisa diterapkan pada sebuah aplikasi pencari rute jalan yang terdekat dari suatu daerah ke daerah lainnya. dengan metode ini hasil yang di dapat bisa lebih optimal namun memelukan resource yang cukup besar jika dipakai untuk pencarian yang kompleks.
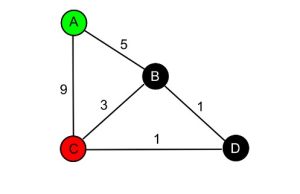
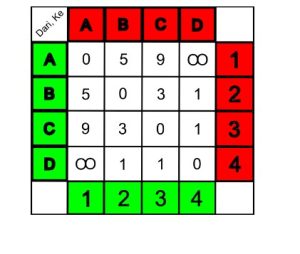
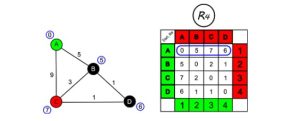
Langkah pertama kita jadikan grafik di atas menjadi sebuah tabel atau matriks.
Kotak abjad berwarna hijau disamping kiri adalah titik awal dan kotak abjad berwarna merah yang ada di atas adalah titik tujuan-nya. Sedangkan kotak angka hijau dan merah berfungsi untuk menentukan sebuah index proses (R0=1,R1=2,R2=3,dan R3=4) dan memudahkan posisi angka-angka yang ada didalam tabel dengan mengkombinasikan-nya dengan kotak abjad yang sama dengan warnaya. sebagai contoh :
A(3),B(2) (titik awal, titik tujuan) = 9,0
Karena dalam grafik diatas terdapat 4 buah titik, yaitu A, B, C, D maka akan ada 5 proses yang akan dilewati yaitu R0, R1, R2, R3, dan R4 sebagai hasil akhir. perlu diingat bahwa hasil dari sebuah proses akan digunakan untuk proses berikutnya.
Rumusnya adalah :
r = Index proses. => R0 = 1, R1 = 2, R2 = 3, R3 = 4, R4 adalah hasil akhir.
S = Titik awal. => A, B, C, dan D (kotak hijau).
E = Titik tujuan. => A, B, C, dan D (kotak merah).
” jika hasil penjumlahan nilai titik awal S(r) dan nilai titik tujuan E(r) lebih kecil daripada nilai jarak yang sebenarnya S(E), maka ganti nilai jarak sebenarnya dengan hasil penjumlahan nilai titik awal dan nilai titik tujuan [ S(E) = S(r) + E(r) ] “.
Jadi, Saya akan mencontohkan sebagian penerapan rumus diatas untuk proses pertama yaitu R0.
r = R0 = 1
S = { A(r) = 0 ; B(r) = 5 ; C(r) = 9 ; D(r) = tak hingga }
E = { A(r) = 0 ; B(r) = 5 ; C(r) = 9 ; D(r) = tak hingga }
– Titik awal A ke titik tujuan A => A(A) = 0
A(r) + A(r) = 0 + 0 = 0 => 0 sama dengan A(A) <tidak diganti>
– Titik awal A ke titik tujuan B => A(B) = 5
A(r) + B(r) = 0 + 5 = 5 => 5 sama dengan A(B) <tidak diganti>
– Titik awal A ke titik tujuan C => A(C) = 9
A(r) + C(r) = 0 + 9 = 9 => 9 sama dengan A(C) <tidak diganti>
– Titik awal A ke titik tujuan C => A(D) = tak hingga
A(r) + D(r) = 0 + tak hinggga = tak hingga => tak hingga sama dengan A(D) <tidak diganti>
– Titik awal B ke titik tujuan A => B(A) = 5
B(r) + A(r) = 5 + 0 = 5 => 0 sama dengan B(A) <tidak diganti>
– Titik awal B ke titik tujuan B => B(B) = 0
B(r) + B(r) = 5 + 5 = 10 => 10 lebih besar dari B(B) <tidak diganti>
– Titik awal B ke titik tujuan C => B(C) = 3
B(r) + C(r) = 5 + 9 = 14 => 14 lebih besar dari B(C) <tidak diganti>
– Titik awal B ke titik tujuan C => B(D) = 1
B(r) + D(r) = 5 + tak hinggga = tak hingga => tak hingga lebih besar dari B(D) <tidak diganti>
– Titik awal C ke titik tujuan A => C(A) = 9
C(r) + A(r) = 9 + 0 = 9 => 9 sama dengan C(A) <tidak diganti>
– Titik awal C ke titik tujuan B => C(B) = 3
C(r) + B(r) = 9 + 5 = 14 => 14 lebih besar dari C(B) <tidak diganti>
– Titik awal C ke titik tujuan C => C(C) = 0
C(r) + C(r) = 9 + 9 = 18 => 18 lebih besar dari C(C) <tidak diganti>
– Titik awal C ke titik tujuan C => C(D) = 1
C(r) + D(r) = 9 + tak hinggga = tak hingga => tak hingga lebih besar dari C(D) <tidak diganti>
– Titik awal D ke titik tujuan A => D(A) = tak hingga
D(r) + A(r) = tak hingga + 0 = tak hingga => tak hingga sama dengan D(A) <tidak diganti>
– Titik awal D ke titik tujuan B => D(B) = 1
D(r) + B(r) = tak hingga + 5 = tak hingga => tak hingga lebih besar dari D(B) <tidak diganti>
– Titik awal D ke titik tujuan C => D(C) = 1
D(r) + C(r) = tak hingga + 9 = tak hingga => tak hingga lebih besar dari D(C) <tidak diganti>
– Titik awal D ke titik tujuan C => D(D) = 0
D(r) + D(r) = tak hingga + tak hinggga = tak hingga => tak hingga lebih besar dari D(D) <tidak diganti>
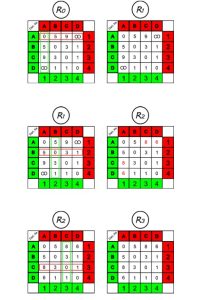
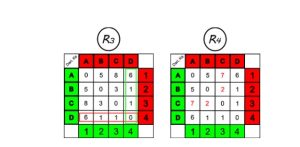
Demikianlah proses dari R0. Tidak ada yang diganti karna tidak ada hasil penjumlahan yang menunjukkan lebih dari nilai jarak sebenarnya S(E). Untuk proses selanjutnya sampai proses hasil akhir R4 saya presentasika melalui gambar di bawah ini.
Dari hasil tabel matriks R4 dapat diketahui rute terpendek manakah yang harus ditempuh dari titik A menuju ke titik C. kemudian kita tulis nilai-nilai yang ada di table matriks R4 disamping titik dalam grafik sesuai dengan abjab mereka.
Untuk mengetahui bagaimana kita mendapatkan urutan rute mana saja yang harus kita lewati, kalian bisa melihat artikel yang sebelumnya tentang Algoritma Dijkstra pada bagian “Cara mengetahui rute yang harus dilewati”
Berikut Merupakan Contoh makalah Penerapan Algoritma Floyd Warshall
MENENTUKAN RUTE TERPENDEK DENGAN MENGGUNAKAN ALGORITMA FLOYD